公交车辆调度问题是具有复杂约束条件的组合优化问题,需要将车辆、客流、服务、运营等因素考虑到公交调度方案中,以此建立多目标车辆调度模型。运用粒子群优化算法(PSO)进行比较分析并求解车辆调度问题,制定公交车辆调度方案。
1、粒子群算法
2、粒子群算法流程
粒子群算法主要解决优化问题,通过生成一群随机的粒子,并通过多次迭代来找到解。每个寻优问题的解被称为粒子,每个粒子在搜索空间中单独地搜寻解适应值,并将个体适应值与整个粒子群里的其他粒子共享,找到当前全局解。粒子群算法流程主要分为初始化粒子群、计算适应值、求个体适应值、寻找全局解和更新粒子的速度和位置。
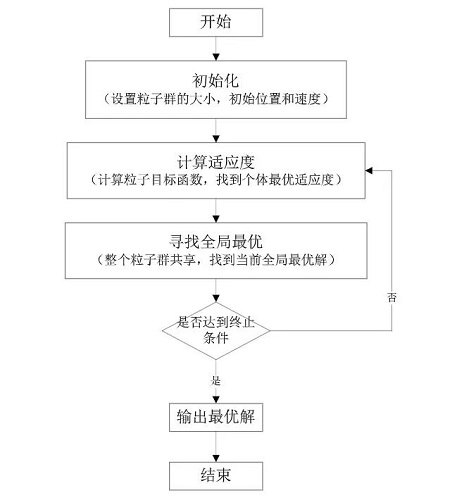
3、公交车辆调度的粒子群算法
在建立车辆调度模型时,要将实际问题进行数学化,选取某条线路公交车总里程L,并设定公交车辆的车型、发车间隔、运行时间等条件,将公交车辆的运营时间分为K个时段,第K个时段的发车间隔为△t_k。设定模型约束条件时优先考虑乘客服务水平,将乘客的等待时间短为出发点,同时也考虑运营成本化,根据两个目标函数的权值问题,结合各站点客流量及运营条件求解此条路线的车辆运行时刻表。
| 算法公式为: |
|
根据粒子群算法合理解决公交排班系统问题,需要将人、车、路等因素考虑进去,运用科学算法解决公交调度问题。公交车排班是调度系统的核心内容,合理的发车时刻表可以提高车辆利用率,降低运营成本,减少乘客候车时间。
4、结语
通过粒子群算法并结合其他智能优化算法,能够在合理的时间里根据设定条件得到解,尤其在车辆调度问题上,随着数据量的增加,通过一系列智能优化算法得出满意的车辆调度方法,合理确定发车时间和车次,优化发车密度,化满足乘客出行需求。
本文转载城市公共交通公众号。
声明:本网站发布内容和图片的目的在于传播更多信息,归原作者所有,不为商业用途,如有侵权敬请作者与我们联系删除。
上一条 : 济南公交“四大生态建设”的实践探索
下一条 : 数字人民币又有大消息!